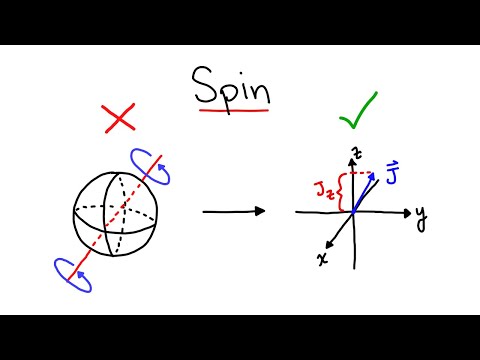
Spin
Francis Villatoro: El espín para irreductibles. Naukas - eitb.eus
twitter BTeseracto/status/1520085494071238660
Se suele describir al spin como el momento angular intrínseco de una partícula. Pero las partículas ni son bolitas ni están girando. La explicación requiere de física experimental, mecánica cuántica, teoría de grupos y muchas ganas. Así que vamos allá ¿Qué es el spin?
Pongámonos en contexto, año 1922, una época en la que el desarrollo de la mecánica cuántica aún estaba en tareas pendientes y a los científicos Stern y Gerlach les dio por hacer pasar átomos de plata a través de un campo magnético variable.
En ese momento, el modelo atómico prevalente era el de Bohr, que describía los átomos como un núcleo rodeado por electrones que orbitaban a su alrededor en órbitas muy definidas (cuantizadas). Algo similar al sistema solar. Esto hoy no se da como correcto.
El átomo de plata tiene 47 electrones, 46 de ellos en sus primeros 4 niveles energéticos, lo que deja al último electrón solo en el siguiente nivel. Clásicamente hablando, esto genera un momento dipolar, algo similar a un imán.
Debido a esto, al pasar los átomos a través del campo magnético, este “dipolo” debería interactuar con el campo y desviar su trayectoria en una dirección aleatoria, pues cada átomo tendría una posición diferente. Creando así una distribución uniforme en la pantalla final.
Lo que encontraron lo podemos ver en la imagen adjunta, extraída del artículo de Stern y Gerlach. A la izquierda sin campo magnético, a la derecha con un campo variable no homogéneo. Un resultado que aún no podían explicar, pues no contaban con la mecánica cuántica.
La interpretación a la que pudieron llegar después de años fue que estas partículas debían de tener alguna especie de momento angular interno en alguna clase de espacio interno. Esto explicaría las observaciones. A partir de aquí las cosas se pusieron aún más raras.
Hasta aquí llega lo que quizás hayáis visto otras veces, el spin como momento angular de la partícula. Sonaría muy bien si estas fueran bolitas, pero no es el caso.
Podríamos haberlo dejado aquí y no habernos metido en este berenjenal, pero ya puestos, juguemos al juego de ver hasta dónde podemos llegar. Eso sí, no podemos prometer que no duela.
El spin es un efecto puramente cuántico, sin ningún tipo de homólogo clásico y sin nada en nuestra intuición física para apoyarnos. Lo único que tenemos es la mecánica cuántica. Así que ahí es donde nos tenemos que meter.
En mecánica cuántica a cada observable le corresponde un operador. En el caso del electrón, tenemos 3 observables, que son el spin en los 3 ejes de coordenadas (x,y,z). En este caso serán matrices de dimensión dos, puesto que hay dos valores posibles que el spin puede tomar.
Necesitamos determinar cómo son estas matrices para poder trabajar con el spin en este espacio. Una de ellas es relativamente obvia, pues sabemos por los postulados de la mecánica cuántica que los valores propios de un operador son los resultados posibles de una medida.
Esto nos permite determinar una de las matrices, se suele escoger el operador del spin en la dirección z. Con ello tendremos una matriz diagonal con los dos valores posibles del spin. Valores que se han podido medir gracias al experimento de Stern y Gerlach.
¿Qué sabemos de las otras dos? Nada. Lo que sí que sabemos es que las matrices de rotación en nuestro espacio clásico de toda la vida son las generadoras del momento angular, con lo cual vamos a postular que los operadores de spin están relacionados con ellas.
Como ya hemos dicho, aquí ya no sirve nuestra intuición física. Debemos recurrir a las matemáticas, más concretamente a la teoría de grupos. Pero antes de nada ¿qué es un grupo?
Un grupo es una estructura algebraica formada por un conjunto cualquiera con una ley de composición interna. Una ley de composición interna es una aplicación que asocia una pareja de elementos de un conjunto a un único valor de ese conjunto.
El conjunto tiene que cumplir tres condiciones: tiene que ser asociativo, que su elemento neutro no lo cambie y que la aplicación por su inverso dé el elemento neutro. Esto se verá muy fácilmente con un ejemplo.
El conjunto de los números enteros con la suma forma un grupo. Puedes coger tres números enteros y sumarlos en el orden que quieras sin cambiar el resultado, es asociativo. Cualquier entero más cero es el mismo número y cualquier entero más su negativo da cero.
En cambio, el conjunto de los números naturales con la suma no sería un grupo puesto que no tiene elementos simétricos que son los números negativos. Después de este inciso, volvamos al spin.
El grupo que nos interesa para resolver este problema es el llamado SO3, que contiene las rotaciones en un espacio tridimensional sobre el origen de coordenadas. Está relacionado con el grupo SU2, que tiene las matrices que nos interesan.
La importancia de esto es la relación de conmutación que cumple este grupo. El conmutador es la multiplicación de los operadores en un orden menos su multiplicación en el orden inverso (Recordemos: la matriz resultante de A por B no tiene por qué ser igual que la de B por A).
Ejemplo general de cómo funciona un conmutador. Entre corchetes tenemos O sub 1, 0 sub 2. Esto es igual a la multiplicación del primero por el segundo menos la multiplicación del segundo por el primero. Si la multiplicación en ambos sentidos da el mismo resultado el conmutador será nulo, en caso contrario será no nulo.
Si el orden de los factores altera el producto el conmutador es no nulo.
Y es justamente el caso de estas matrices. A esto lo consideramos la relación de conmutación fundamental del momento angular y partimos de la base de que los operadores del Spin también cumplirán esta relación de conmutación.
Por tanto, solo necesitamos encontrar las matrices dos por dos que cumplan estas relaciones. Las tres matrices son estas. Y son lo que necesitamos para poder hacer cálculos con el spin ½.
Como puede verse, los conmutadores entre los diferentes operadores del spin son no nulos lo que implica que son incompatibles, la medida de uno te rompe la del otro. Igual que pasa con la posición y el momento, es algo que sucede con frecuencia en mecánica cuántica.
Estos operadores nos van a describir la rotación del espacio de los spines y, por tanto, es lo que necesitamos para trabajar con ellos. En el caso del electrón (spin ½) las matrices son dos por dos, si el spin fuese 1 la matriz sería tres por tres, y así sucesivamente.
Si has llegado hasta aquí (gracias) tal vez te preguntes si toda esta explicación era necesaria. Después de darle muchas vueltas (perdón) hemos creído que sí. Así es como se entiendo el spin en mecánica cuántica. No hay ningún tipo de homólogo clásico sobre el que apoyarnos.
Las partículas ni son bolitas ni dan vueltas y la forma que tenemos de entender que tengan un momento angular es esta. Y podemos ir más allá, porque en última instancia (hasta donde sabemos) las partículas son perturbaciones de campos cuánticos.
La teoría cuántica de campos es una teoría cuántica relativista (con la especial, no con la general). En este marco el spin aparece de forma natural. De haber contado con la teoría cuántica de campos, podrían haber predicho el resultado del experimento de Stern y Gerlach.
Y de aquí podemos extraer el teorema de la estadística del spin. Las partículas con spin fraccionario (½, 3/2…) siguen la estadística de Fermi-Dirac, con lo que son fermiones. Las que tienen el spin entero siguen la de Bose-Einstein, son bosones.
El spin lo condiciona todo, desde la química hasta las interacciones fundamentales de la naturaleza. Aunque es puramente cuántico y sin mecánica cuántica no lo podemos describir, sigue siendo una pieza fundamental del universo tal y como lo conocemos.