Recursos física cuántica
Recursos generales
Ver apuntes de elaboración propia de Física de 2º de Bachillerato Se utiliza el término física cuántica aunque a veces se habla de mecánica cuántica.
Puede haber recursos relacionados en recursos física nuclear y en recursos física de partículas
- Cuántica sin fórmulas
http://eltamiz.com/2007/09/04/cuantica-sin-formulas-preludio/
Pedro Gómez-Esteban, eltamiz.com, Licenciamiento cc-by-nc-nd. Serie de artículos (desde 2007 a 2010) muy recomendables. - Física cuántica
Bienvenidos a hbarra
Esta página ha surgido como parte de un proyecto docente dedicado a la adaptación de las asignaturas de Física Cuántica y Mecácnica Cuántica, de la licenciatura de Física, a las nuevas tecnologías. Autor José Ignacio Fernández Palop, Profesor Titular de la Universidad de Córdoba y profesor encargado de las asignaturas de Física Cuántica y Mecánica Cuántica de la Licenciatura de Física, Licenciamiento no detallado. - Oxford-University Reading: Quantum Mechanics. Vídeos (ogg, mp4) con clases sobre Mecánica Cuántica
Oxford-University Reading: Quantum Mechanics : Free Download, Borrow, and Streaming : Internet Archive
In this series of physics lectures, Professor J.J. Binney explains how probabilities are obtained from quantum amplitudes, why they give rise to quantum interference, the concept of a complete set of amplitudes and how this defines a “quantum state”.
001 Introduction to Quantum Mechanics, Probability Amplitudes and Quantum States
002 Dirac Notation and the Energy Representation
003 Operators and Measurement
004 Commutators and Time Evolution (the Time Dependent Schrodinger Equation)
005 Further TDSE and the Position Representation
006 Wavefunctions for Well Defined Momentum, the Uncertainty Principle and Dynamics of a Free Particle
007 Back to Two-Slit Interference, Generalization to Three Dimensions and the Virial Theorem
008 The Harmonic Oscillator and the Wavefunctions of its Stationary States
009 Dynamics of Oscillators and the Anharmonic Oscillator
010 Transformation of Kets, Continuous and Discrete Transformations and the Rotation Operator
011 Transformation of Operators and the Parity Operator
012 Angular Momentum and Motion in a Magnetic Field
013 Hilary: The Square Well
014 A Pair of Square Wells and the Ammonia Maser
015 Tunnelling and Radioactive Decay
016 Composite Systems - Entanglement and Operators
017 Einstein-Podolski-Rosen Experiment and Bell’s Inequality
018 Angular Momentum
019 Diatomic Molecules and Orbital Angular Momentum
020 Further Orbital Angular Momentum, Spectra of L2 and LZ
021 Even further Orbital Angular Momentum - Eigenfunctions, Parity and Kinetic Energy
022 Spin Angular Momentum
023 Spin 1/2 , Stern - Gerlach Experiment and Spin 1
024 Classical Spin and Addition of Angular Momenta
025 Hydrogen part 1
026 Hydrogen part 2 Emission Spectra
027 Hydrogen part 3 Eigenfunctions
- La Física Cuántica explicada en 5 minutos (VIDEO) Principia Marsupia
la-fisica-cuantica-explicada-en-5-minutos-video / - Quantum Mechanics: Animation explaining quantum physics.

Eugene Khutoryansky. Covers all the topics, including wave particle duality, Schrodinger’s cat, EPR / Bell inequality, and the relationship between measurement and entanglement. - Quantum made simple
Tout est quantique - Einstein_frente_a_la_teoria_cuantica.pdf
J.L.Sánchez-Gómez, Dpto. Física Teórica Univ. Autónoma de Madrid. 
- Revolución cuántica (51 min, documental odisea)

- La teoría cuántica (1ª parte) tan precisa… y tan sorprendente (51 min)

Se pueden citar también cursos (ver página de cursos online), libros …
En 2014 se imparte un curso de mecánica cuántica para estudiantes de Bachillerato en el IES San Mateo, y ojear el contenido es interesante
La Física en el Bachillerato de Excelencia: Mecánica Cuántica para estudiantes de bachillerato
Curso de Mecánica Cuántica para estudiantes de bachillerato - lista vídeos YouTube
Hay vídeos introductorios / generales, por ejemplo
¿Qué es la mecánica cuántica? Date un Voltio

Dos experimentos verifican que la mecánica cuántica requiere números complejos
twitter CaRoLCrEsPo_FyQ/status/1553765783632846849
En 1925-26 nace la Mecánica Cuántica. Justo antes en 1925 Pauli publica el principio de exclusión. Posteriormente su visión del espín y su comportamiento se integrarían en la Mecánica Cuántica. Aquí una línea de tiempo con los acontecimientos históricos previos:
Heisenberg y Schrödinger con sus trabajos inician la Mecánica Cuántica. #ciencia @scientix_eu
Conferencia de Solvay 1927
The Solvay Conference, probably the most intelligent picture ever taken, 1927 - Rare Historical Photos
Solvay Physics Conference 1927

https://twitter.com/PramodhYapa/status/1335710125332393987
So this took entirely too much time (especially doing the terrible Zoom background blur), but here is my gift to the Physics community.
I present to you, Solv(irtual)ay 2020!

Principio de incertidumbre
What is the Uncertainty Principle? MinutePhysics
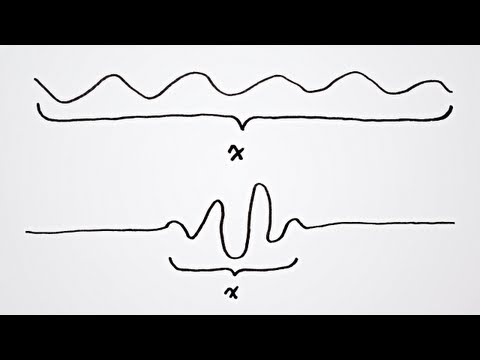
Heisenberg’s Uncertainty Principle Explained. Veritasium
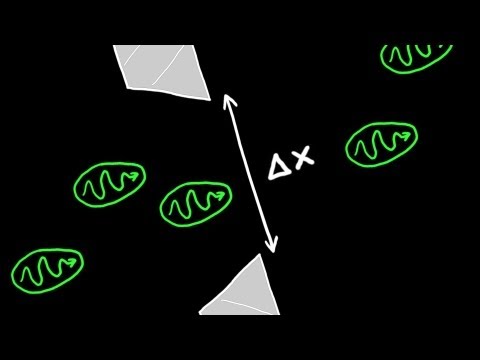
twitter emulenews/status/1280377545586814976
Sobre las Relaciones de Incerteza de Heisenberg entre Tiempo y Energía: Una nota didáctica, por @GastonGiribet, del curso introductorio a la mecánica cuántica dictado en la Facultad de Ciencias Exactas y Naturales de la Universidad de Buenos Aires
[physics/0506001] On the Energy-Time Uncertainty Relations: A didactical note for undergraduate students
On the Energy-Time Uncertainty Relations: A didactical note for undergraduate students
twitter DivulgaMadrid/status/1591905376966176768
La primera vez que vi en mi vida una alusión al principio de indeterminación de Heisenberg fue en mi libro de texto de FyQ en Bachillerato. El libro lo explicaba con la desigualdad de la imagen. Pero esta desigualdad NO ES EL PRINCIPIO DE INDETERMINACIÓN.
Abro hilo
Electro Dinámica Cuántica EDC (QED Quantum Electro Dinamics)
Quantum electrodynamics - wikipedia
Collective Molecular Dynamics of a Floating Water Bridge
When a high voltage is applied to pure water filling two beakers kept close to each other, a connection forms spontaneously, giving the impression of a floating water bridge. This phenomenon is of special interest, since it comprises a number of phenomena currently tackled in modern water science. The formation and the main properties of this floating water bridge are analyzed in the conceptual framework of quantum electrodynamics. The necessary conditions for the formation are investigated as well as the time evolution of the dynamics. The predictions are found in agreement with the observations.
How To Defy Gravity With Water | THE WATER BRIDGE EXPERIMENT|

Efecto Casimir
El efecto Casimir: explicación con vídeos – Ciencia explicada
Dualidad onda-corpúsculo
Efecto túnel
Relacionable con desintegración nuclear y con principio de incertidumbre
Tout est quantique
Láser
Gato de Schrödinger

También cabe algo de humor …
Viñeta genial de Igor Fernández, publicada en El Jueves.
twitter igor_f_f/status/505316690822180864
Detector bombas Elitzur-Vaidman
http://eltamiz.com/2010/07/21/cuantica-sin-formulas-el-detector-de-bombas-de-elitzur-vaidman/
Medida sin interacción
Imágenes de objetos con fotones que no interaccionan con ellos de forma directa - La Ciencia de la Mula Francis
http://cuentos-cuanticos.com/2014/08/27/gato-no-te-escondas-que-te-voy-fotografiar-igual/
Desigualdades de Bell
Bell’s Theorem: The Quantum Venn Diagram Paradox - MinutePhysics 3Blue1Brown

Algo sobre la luz y la mecánica cuántica (con MinutePhysics) 3Blue1Brown
[
Medida débil
How the result of a measurement of a component of the spin of a spin-1/2 particle can turn out to be 100. Aharonov 1988 - isy.liu.se
Efecto Aharonov-Bohm
Aharonov–Bohm effect - Wikipedia
Campo y partícula
Francis en @TrendingCiencia: La realidad está hecha de campos, no de partículas - La Ciencia de la Mula Francis Los conceptos de campo, partícula, partícula virtual y vacío - La Ciencia de la Mula Francis
mas-pruebas-que-electron-se-comporta-como-si-estuviera-compuesto-por-dos-particulas Dos campos cuánticos
https://twitter.com/emulenews/status/1395064528522682376
¿El qué? ¿La separación de una cuasipartícula de tipo electrón (una onda de electrones) en tres componentes llamadas espinón, orbitón y holón (o cargón)? ¿O que el campo cuántico del electrón tenga dos componentes (en realidad tiene cuatro, dos del electrón y dos del positrón)?
Materiales de Guillermo García Alcaine, Departamento Física Teórica UCM
Algunos de estos materiales están asociados a un curso de mecánica cuántica que realicé en 2011 y en el que Guillermo García Alcaine era uno de los ponentes.Considero que son muy interesantes los materiales que aclaran conceptos sin usar fórmulas (como el curso de Cuántica sin fórmulas de El Tamiz), y como en 2015 no localizo estos materiales por internet los coloco aquí; no indican licenciamiento explícitamente pero dejando clara su atribución no creo que haya problemas, y dejo clara mi disponibilidad a retirarlos si los hubiera.
Algunas preguntas sobre Mecánica Cuántica, Guillermo García Alcaine (PDF 16 páginas) Adversus colapsum, Guillermo García Alcaine, Gabriel Álvarez (PDF 18 páginas) , (quizá es el mismo que se cita aquí Adversus collapsum | García Alcaine | Revista Española de Física ) Mecánica cuántica para filósofos, Guillermo García Alcaine (PDF 9 páginas) Hay otros materiales que no pongo localmente aquí / sí se pueden encontrar públicamente / no asociados a ese curso: Einstein y la Mecánica Cuántica, Monografías de la Real Academia de Ciencias de Zaragoza. 27: 97–118, (2005).
Guillermo García Alcaine, “Enredo Cuántico,” [PDF] Zse8f5
Guillermo García Alcaine, Gabriel Álvarez Galindo, “Localidad einsteiniana y mecánica cuántica,” [PDF] 5ps6K1
Recursos laboratorios no virtuales
Son laboratorios “avanzados” que requieren material especial
MIT OpenCourseWare
Experimental Physics I & II “Junior Lab”
Introductory experiment 2: Photoelectric effect lab2
Photoelectric effect lab guide jlexp005.pdf
cc-by-nc-sa
Más laboratorios en el mismo curso: Compton, …
Computación cuántica
Entrelazamiento
Tú no sabes por qué sale cara, pero la moneda sí
ER = EPR - wikipedia
Un ordenador cuántico logra recrear un agujero de gusano gravitacional - eldiario.es
Traversable wormhole dynamics on a quantum processor - nature.com
Gravedad cuántica
New theory seeks to unite Einstein’s gravity with quantum mechanics - ucl.ac.uk
Recursos laboratorios virtuales / simulaciones
Radiación del cuerpo negro / Ley Steffan- Boltzmann / Ley Wien / Planck
Espectro del Cuerpo Negro
blackbody-spectrum
Enlace directo sin descarga Espectro del Cuerpo Negro 2.02
 6:29 se comenta catástrofe ultravioleta
6:29 se comenta catástrofe ultravioleta
12:10 se comenta idea estabilidad átomo
13:10 imagen espectro con colores y saltos
14:20 imagen longitud de onda de Broglie
radiazione del corpo nero (italiano)
corponero.htm
Universitá degli Studi Messina
Se visualiza bien el cambio de color con el cambio de temperatura
Planck Law Radiation Distributions
planck.html
Blackbody Radiation Exercises
Blackbody Radiation Exercises
BlackBody: The Game!
BlackBody: The Game!
Applet: Blackbody Spectrum
black.htm
© W. Bauer, 1999
Black Body Radiation
BBR.html
Efecto fotoeléctrico
Physique et simulations numériques.
Physique et simulation
Jean-Jacques ROUSSEAU. Faculté des Sciences exactes et naturelles. Université du Maine
Francés. Niveaux : Lycée, premier et second cycles.
Effet photoélectrique
Efecto fotoeléctrico (HTML5) Permite potencial frenado y varios metales
The Open Source Physics Project.
Photoelectric Effect Model
Photoelectric Effect Model
written by Jose Ignacio Fernández Palop
Incluye potencial de frenado photoelectric (JNLP, funciona con Web Start, necesita java instalado) Los metales permitidos son Na, Zn, Cu, Pt, Ca.
El Efecto Fotoeléctrico (versión HTML5) Efecto fotoeléctrico | Educaplus Applet: Photo Effect
photo.htm
© W. Bauer, 1999
PhotoElectric Effect Simulator, OpenSourcePhysicsSG
PhotoElectric Effect Simulator - Apps on Google Play
Modelo atómico de Bohr
Teoría de Bohr del Átomo de Hidrógeno Teoría de Bohr del Átomo de Hidrógeno (versión HTML5)© Walter Fendt, 30 Mayo 1999
© Traducción: José M. Zamarro, 24 Noviembre 2001
Interesante la visualización en “modelo onda”
Bohr Atom
app.htm
© W. Bauer, 1999
Luces de Neón y otras Lámparas de Descarga
discharge-lamps
Simulación donde se visualizan saltos electrónicos y el espectro
© W. Bauer, 1999
interazione radiazione-materia (italiano)
photon_ita.htm
Original applet © 1997 by Sergey Kiselev and Tanya Yanovsky-Kiselev
Adapted applet © 1998 by Carlo Sansotta for IFMSA WebLab
Experimento de Stern-Gerlach
Physique et simulations numériques.
Physique et simulation
Jean-Jacques ROUSSEAU. Faculté des Sciences exactes et naturelles. Université du Maine
Francés. Niveaux : Lycée, premier et second cycles.
Expérience de Stern et Gerlach Tout est quantique Vídeo sobre spin que reproduce experimento Stern-Gerlach
Spin
Cuántica y química
Enlaza con la idea de química física y física química
First reported case of hydrosilane activation mediated by hydrogen quantum tunnelling
Láser
Ver simulaciones en Láser
Efecto Compton
Physique et simulations numériques.
Physique et simulation
Jean-Jacques ROUSSEAU. Faculté des Sciences exactes et naturelles. Université du Maine
Francés. Niveaux : Lycée, premier et second cycles.
Effet Compton effetto Compton (italiano)
compton.htm
Universitá degli Studi Messina
Original applet © by Jan Humble
Adapted applet © 2001 by Carlo Sansotta for IFMSA WebLab
http://ressources.univ-lemans.fr/AccesLibre/UM/Pedago/physique/02/divers/compton.html
Orbitales
Ver recursos sobre orbitales
http://ressources.univ-lemans.fr/AccesLibre/UM/Pedago/physique/02/mndivers.html
Interpretaciones mecánica cuántica
twitter DivulgaMadrid/status/1599867528297078784
Adivinanza:
¿Quién dijo esto en 1955?
twitter DivulgaMadrid/status/1599417208685268992
Un “debate científico” fue lo de Bohr y Einstein. Y ganó Bohr.
Nosotros sólo somos unos pringaos que dicutimos en Twitter el significado de los conceptos de una teoría bien establecida que tiene ya casi 100 años.
Esto no va de quién la tiene más grande (la interpretación).
Yo sólo hablo de esto para seguir desarrollando herramientas para enseñar la mecánica cuántica. Por favor, no llaméis a lo que digo “tu interpretación”. No es mía. Es de los fundadores de la cuántica. No tiene ningún mérito científico lo que digo. No aporto nada nuevo.
twitter DivulgaMadrid/status/1581538128233316354
Y otra confusión es pensar que el no realismo dice que no existe la realidad física o el objeto físico. Sí existe, sólo que sus observables no son una característica sólo de él, sino también, por ejemplo, en el spin, de en qué dirección orientes el aparato.
twitter DivulgaMadrid/status/1594425171552702465
En la integral de camino de Feynman sumamos para todos los caminos. Pero, en cada uno, posición y momento toman siempre valores bien definidos. ¿Podemos por eso construir una interpretación “realista” de la mecánica cuántica?
¡La tabla periódica nos da una respuesta!
twitter DivulgaMadrid/status/1599877706745012224
La mecánica cuántica es difícil de enseñar. Los profesores tenemos que estar continuamente aclarando lo que decimos, porque la probabilidad de que algo se malinterprete es alta. Por ejemplo, se oye mucho que una superposición significa que el gato está vivo y muerto a la vez.
…
Libros
twitter SrinivasaR1729/status/1803086273026167273
I recommend these 4 books to get a solid grasp of the basics of mathematics in quantum mechanics. Perfect for general readers and beginners!
- Introduction to Quantum Mechanics, David J. Griffiths.
- ‘Quantum Mechanics: The Theoretical Minimum’ by Leonard Susskind.
- ‘Quantum Mechanics for Scientists and Engineers’ by David A.B. Miller.
- ‘Principles of Quantum Mechanics’ by R. Shankar. I



