Física y Química‎ > ‎Recursos‎ > ‎Recursos Física‎ > ‎

Teoría del caos


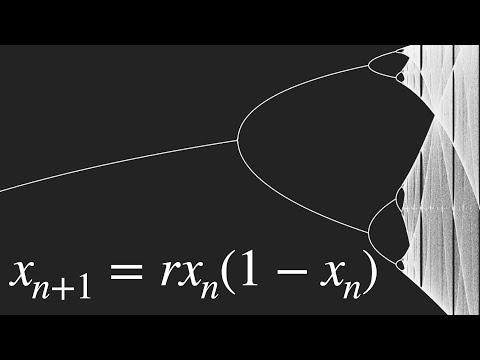
En el currículo de Física de 2º de Bachillerato LOMCE se introduce "caos determinista", "7. Interpretar el caos determinista en el contexto de la interacción gravitatoria.", "7.1. Describe la dificultad de resolver el movimiento de tres cuerpos sometidos a la interacción gravitatoria mutua utilizando el concepto de caos."

Aunque históricamente la idea de caos surge en gravitación y asociado al problema de los tres cuerpos, es algo más general y que aplica a varias disciplinas además de la física.
Uno de los precursores fue Poincaré, que presentó un estudio sobre la estabilidad del Sistema Solar como parte de un concurso en el siglo XIX
https://es.wikipedia.org/wiki/Henri_Poincar%C3%A9#El_problema_de_los_tres_cuerpos
Un caso importante es el problema restringido, en el que la masa de uno de los tres objetos es despreciable, que tiene a su veces otros casos como el problema restringido circular
En la solución del problema restringido circular surgen 5 puntos de equilibrio que se llaman puntos de Langrange y se numeran de L1 a L5
https://es.wikipedia.org/wiki/Puntos_de_Lagrange
Son puntos de utilidad directa: en L1 está SOHO (Solar and Heliospheric Observatory) y en L2 está Wilkinson Microwave Anisotropy Probe (WMAP) (NASA)
Existen algunas soluciones concretas (en 1993 se encontró una solución con trayectoria en forma de 8)

En general la teoría del caos sin pensar solamente en gravitación se puede ver como un caso de dinámica no lineal. Dinámica no hace referencia solamente a movimiento de cuerpos, sino en "evolución del valor de una variable de un sistema". Aplica a movimiento de osciladores no lineales (péndulo doble, péndulo magnético), evolución de poblaciones, economía, dinámica de fluidos, y hay ejemplos matemáticos como el atractor de Lorentz

Aunque se habla de caos, se trata de caos determinista porque el sistema aunque es caótico en el sentido de tener un comportamiento que parece poco previsible, sí se pueden encontrar ecuaciones para el movimiento fijadas las condiciones iniciales. Comparando:
Sistemas no caóticos
Sistemas caóticos
Sí existe proporcionalidad: un cambio pequeño en variables produce cambios pequeñosNo existe proporcionalidad: un pequeño cambio puede producir cambios enormes (enlaza con la metáfora del efecto mariposa: el aleteo de una mariposa puede producir un tornado en el otro extremo de la Tierra)
Existe la aditividad/linealidad: el efecto total es la suma de efectosNo existe aditividad/linealidad: el efecto total no es la suma de efectos.
Son reproducibles/previsibles: con condiciones iniciales determinadas se reproduce resultadoNo es reproducible/previsible debido a la alta sensibilidad a las condiciones iniciales, en general es complejo reproducir exactamente y por pequeñas variaciones habrá resultados distintos.

Otras ideas asociadas a sistemas caóticos son:
-Recurrencia: aunque las trayectorias sea erráticas no se pierden en el infinito, sino que vuelven de manera recurrente a ciertos puntos "atractores"
-Autosimilaridad: se producen estructuras que se asemejan a sí mismas a distintas escalas de observación (enlaza con fractales)


Introducción al régimen caótico
Un sistema que experimenta un movimiento caótico nunca se repite a sí mismo, sino que más bien se comporta de forma continuamente diferente, el movimiento puede parecer totalmente aleatorio y desordenado. No obstante, el movimiento caótico está muy lejos de ser totalmente desordenado y por el contrario, exhibe una estructura definida que resulta de pronto aparente. Otro aspecto del caos, es su extrema sensibilidad a las condiciones iniciales que es lo que vamos a ver en esta simulación.


Ejemplos de sistemas caóticos:



Recursos generales


En la píldora 10 de la RSEF se indican recursos sobre "introducción al caos" http://rsef.es/images/Fisica/PildoraFisicaGEEFN10.pdf

Vídeos

Entrevista con James Yorke, el padre de la Teoría del Caos (English)
https://www.youtube.com/watch?v=CBj70zSjKx4

La teoría del caos, explicada con un péndulo. MATERIA Ciencia
https://www.youtube.com/watch?v=d3uOKlIEIoU

Material para demostraciones

http://www.instructables.com/id/The-Chaos-Machine-Double-Pendulum/

https://www.amazon.com/Fat-Brain-Toys-Chaos-Machine/dp/B00PG1MKV0

https://www.amazon.com/American-Educational-Products-6-40020-Packaging/dp/B00BWJ48II

https://www.3bscientific.es/chaotic-pendulum-e-u8557340,p_576_25075.html

http://makezine.com/projects/make-22/double-pendulum/

Simulaciones / ejemplo

Las ecuaciones son complejas, por lo que en Bachillerato se pueden usar simulaciones y ver cualitativamente la dependencia de las condiciones iniciales, la sensibilidad a modificarlas y lo impredecible del comportamiento.

Gravitación - tres o más cuerpos



Mi sistema solar, permite poner más de 2 cuerpos
http://phet.colorado.edu/sims/my-solar-system/my-solar-system_es.html

http://faraday.physics.utoronto.ca/PVB/Harrison/Flash/Chaos/ThreeBody/ThreeBody.html
http://labs.minutelabs.io/Chaotic-Planets/

Péndulo caótico   / péndulo doble

http://labs.minutelabs.io/Chaotic-Pendulum/


Double Pendulum Simulator, OpenSourcePhysicsSG 
https://play.google.com/store/apps/details?id=com.ionicframework.dpendulumapp262907


Pendulum Studio,  Voladd (péndulo en general, incluye péndulo doble) 
https://play.google.com/store/apps/details?id=com.vlvolad.pendulumstudio



Double Double-pendulum, Ashley P. Willis 
https://play.google.com/store/apps/details?id=org.openpipeflow.doubledoublependulum

41 triple pendulums with 𝑠𝑙𝑖𝑔𝘩𝑡𝑙𝑦 different initial conditions

(source:https://external-preview.redd.it/Cp2AZd3V52nIuMQ5WiwV8vg7uuLc6UKjRsA3VZH6ObM.gif?format=mp4&s=345404eed06a65d6138df53328bfdd8c193366fc)


Circuito de Chua


Comments