Cálculo vectorial

Pendiente completar y detallar…
Comentario: el carácter unicode para producto vectorial es “⨯” (U+2A2F)

ISO 80000-2 Quantities and units — Part 2: Mathematical signs and symbols to be used in the natural sciences and technology
Item 2-17.12 indica símbolo es “⨯” (U+2A2F)

Aunque se asocie a matemáticas la idea de vector, a veces se trata pensando solamente en fuerzas sin verlo como general

Relacionado con cinemática y dinámica (momento angular que a veces se llama momento cinético utiliza producto vectorial, y se usa en gravitación (leyes Kepler) y en magnetismo)

En el planteamiento de Docencia contenidos física y química por nivel, visión personal , planteo separar los vectores como un bloque aparte, asociado a magnitudes, a cinemática, a dinámica ….

En el currículo oficial aparece explícitamente

4º ESO LOMCE

…movimiento y la necesidad de un sistema de referencia y de vectores para describirlo adecuadamente…
…los vectores de posición, desplazamiento y velocidad…
…utilizando una representación esquemática con las magnitudes vectoriales implicadas…
…existencia de vector aceleración…
…Naturaleza vectorial de las fuerzas…
…necesidad de usar vectores para la definición de determinadas magnitudes…
…Identifica una determinada magnitud como escalar o vectorial y describe los elementos que definen a esta última…
1º Bachillerato LOMCE
…Distingue entre magnitudes escalares y vectoriales y opera adecuadamente con ellas…

Indirectamente aparece usando magnitudes que son vectoriales o cálculos que implican vectores: momento angular, campo magnético …

Cinemática, escalares y vectores

Escalares y vectores | Educaplus
© 1999-2013, www.educaplus.org

Laboratorio Virtual
Tiene varios apartados, que redirigen a applets:

Suma y resta de vectores

Adición de vectores - phet

Add2Vectors
Add3Vectors
Subtract2Vectors
VectorAddComponents
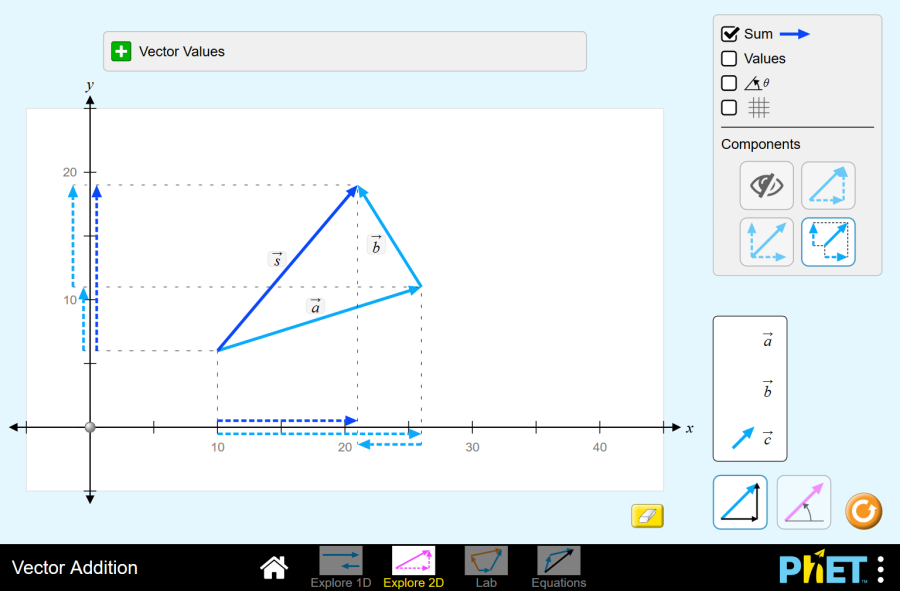
Vector Addition
Composición de Fuerzas (Suma de Vectores) (HTML5)
Suma de Fuerzas Concurrentes | Fisicalab
Tres Fuerzas en Equilibrio
Suma de vectores | Educaplus
Resta de vectores | Educaplus
Se puede usar vectors (4,6) + (7,6) - Wolfram|Alpha

oPhysics: Interactive Physics Simulations
Vector addition
Vector Addition and Subtraction
Vector Addition and Subtraction Practice

Descomposición vectores

Resolución de una Fuerza en sus Componentes

oPhysics: Interactive Physics Simulations
Vector Components

Producto escalar

The Scalar or “Dot” Product of 2 Vectors - utoronto.ca

Producto vectorial

Relacionado con física de 2º de Bachillerato: momento angular (bloque gravitación) y bloque de campo magnético.

A veces se enseña con reglas (de la mano derecha) o como resultado de un determinante

Cross Product and Area Visualization - geogebra.org
Author: Kara Babcock, Wolfe Wall

Applet: Cross product - mathinsight.org

Cross product - animation - youphysics.education

En esta animación se visualiza bastante bien, y utiliza una regla mnemotécnica muy simple, distinta a la de los tres dedos …
Se ponen varios enlaces
The Vector or Cross Product of 2 Vectors - utoronto.ca
The Vector or Cross Product of 2 Vectors - utoronto.ca
David M. Harrison, Dept. of Physics, Univ. of Toronto, Copyright © 2002 - 2011 David M. Harrison, cc-by-nc-sa

crosspro.html
Written by David McNamara, Alan Middleton, and Eric Schiff, Department of Physics, Syracuse University.

EL PRODUCTO VECTORIAL
Juan Francisco González Hernández
Se desarrolla una exposición histórica del origen de la operación que llamamos producto vectorial, destacándose los problemas y conceptos matemática que llevaron a su introducción en el Álgebra. Se incluye una descripción de las más destacadas y representativas aplicaciones de este producto en Física y Matemáticas, así.. como una visión general de las diferentes alternativas para generalizar este producto a espacios de más dimensiones. Finalmente, se discute acerca de la mejor manera de introducir este concepto a nivel teórico y práctico en los .últimos cursos de la E.S.O. y en Bachillerato, destacándose algunos puntos pedagógicos y didácticos que pueden ser de interés práctico

Tensores

Einstein y…la pizarra del Observatorio del Monte Wilson - experientiadocet.com

Un tensor no es más que la extensión del concepto de vector a dimensiones adicionales. Un escalar, un número, aparece en un gráfico como un punto, un objeto de cero dimensiones. Un vector, que tiene magnitud y dirección, aparecería en un gráfico como una línea, es decir, como un objeto de una dimensión. El tensor extiende esta idea a las dimensiones adicionales. Esto podemos interpretarlo como un conjunto de vectores relacionados, moviéndose en múltiples direcciones en un plano.
Lo veremos mejor de otra manera. En vez de pensar en un vector como un conjunto de coordenadas, lo podemos considerar una operación, es decir, un vector lo que haría es asociar una dirección a un número. Lo importante desde el punto de vista matemático es que la operación es lineal y homogénea. Gracias a esto, un vector queda completamente determinado por sus proyecciones en d direcciones, donde d es el número de dimensiones del espacio en el que se define. Por tanto, un vector se puede expresar como un conjunto de números que son en realidad sus proyecciones en un sistema de ejes coordenados.
Un vector es realmente un tensor de rango 1, asocia 1 dirección a un número. Un escalar, es un tensor de rango 0, asocia 0 direcciones a un número. Por tanto un tensor de rango 2 (un tensor ya por derecho propio), asocia dos direcciones arbitrarias a un número. Si quisiéramos expresarlo en términos de las coordenadas, como se hace con los vectores, necesitaríamos d x d números. Para un tensor de rango q, por tanto, necesitaríamos n^q números.